DeepLink
deeplink主要做了以下的事情:
(1)它对网络进行采样,在保持网络结构的同时生成训练“语料库”。
(2)网络中的每个节点通过网络嵌入被表示为低维空间中的一个向量;
(3)然后将锚节点输入深度神经网络,训练非线性变换,使用户跨网络对齐;
(4)DeepLink采用双学习过程来提高身份链接性能,提高监督训练算法。
首先在给定的一对网络a和一对网络B之间预先训练两个初步的映射函数,也就是\(\Phi(A \to B)\)以及\(\Phi^{-1}(B \to A)\)在没有标签(对齐)的锚节点上使用自动映射。然后,用户身份链接可以形式化为一个双重学习游戏:在网络A中的一个铆钉节点的嵌入表示\(\vec a\)可以使用\(\Phi(A \to B)\)得到一个在B中的对应向量\(\vec b'\)。随后向量\(\vec b'\)与其真实的向量\(\vec b\)相比较,和A被通知\(\Phi(A \to B)\)是否是一个高质量的映射,通过使用\(\Phi^{-1}(B \to A)\)将\(\vec b'\)映射回去得到\(\vec a'\)。网络A测量\(\vec a\)和\(\vec a'\)之间的相似度然后反馈给B。游戏也可以从B中的一个节点开始,并在B空间中嵌入向量。本质上,随着锚定节点的增加,这两个映射函数得到了越来越多的改进。
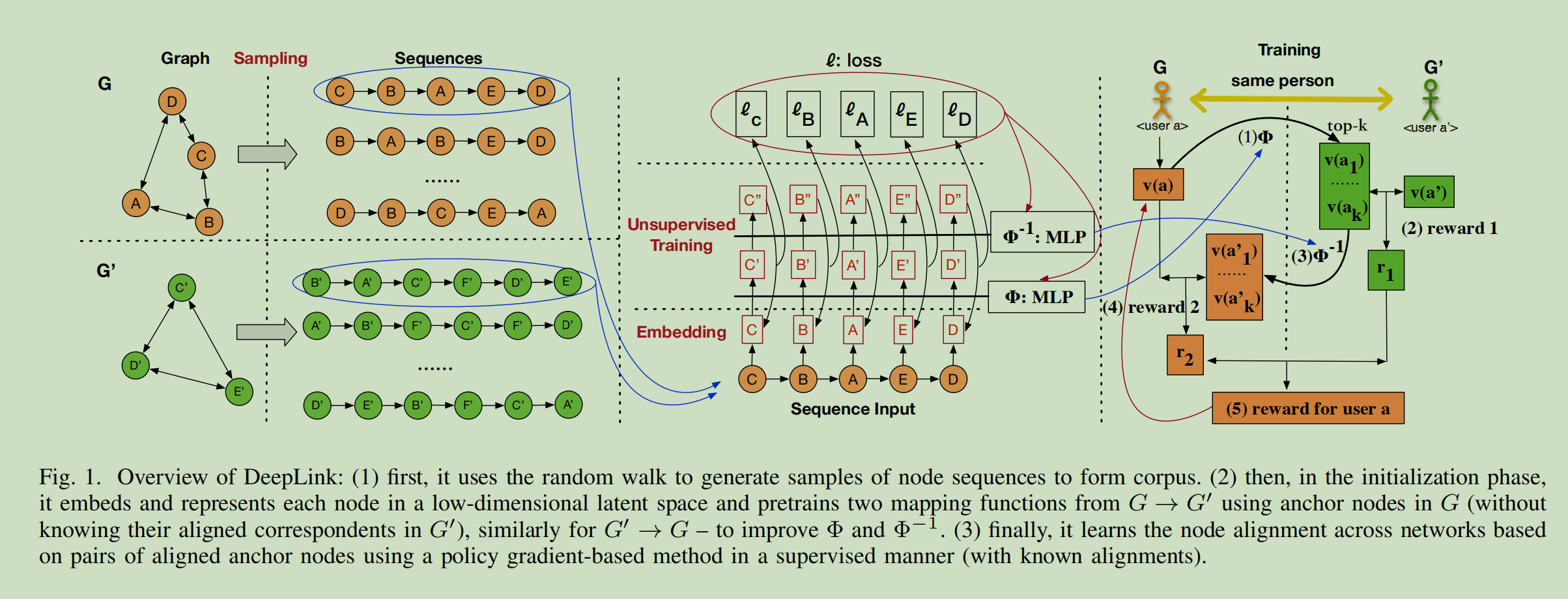
经过随机游走采样得到语句\(S_{u_i}^r\)之后,r表示第r轮次,deeplink使用skip-gram模型来更新embedding。
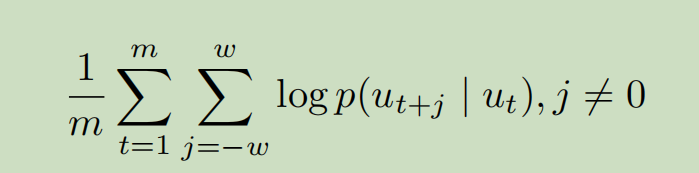
这个公式就是skipgram的优化方程了,网络序列化的一个很重要的概念。w是滑动窗口的大小,条件概率的定义如下:
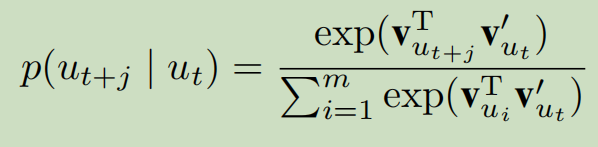
采用负采样后的公式为:

在得到两个网络的embedding之后,deeplink通过MLP学习两个网络之间的映射函数,给定一组标记的anchor node pairs \((u_i,u_j)\)以及其向量\((v(u_i),v(u_j))\),deeplink学习映射\(\Phi(v(u_i))\)通过最小化如下函数:
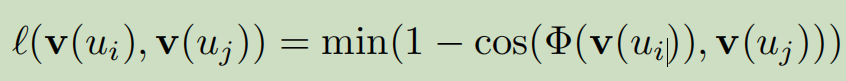
假设A和B是网络节点的向量矩阵,那么优化方程为:
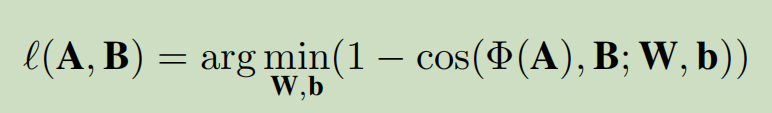
我们要学习的就是W和b,W是权重矩阵,b是偏置。
为了充分利用先验知识的anchor nodes,使用一套dual-learning的机制。假设我们有两个弱映射函数Φ和\(\Phi^{-1}\)例如,用部分锚节点进行预训练-它们可以将向量从Gs投射到Gt,反之亦然。然后,我们改进了两个映射函数
- 无监督UIL预训练:
如果我们首先得到在\(G^s\)中的anchor node的向量\(u_b\),先把他通过\(v'(u_b)=\Phi(v(u_b))\)映射得到\(v'(u_b)\),然后再映射回来通过\(\Phi^{-1}(v'(u_b))\)来得到映射\(v''(u_b)\)。请注意,在这个无监督的学习过程中不需要标签,因此标记锚节点和未标记锚节点之间没有差异。这个自动映射的损失是基于\(v(u_b)\)和\(v''(u_b)\)之间的差值来计算的。我们使用同样的方法对Gt→Gs模型进行预训练。在这个无监督的预训练之后,我们有两个弱映射函数Φ和\(Φ^{-1}\),它们将在下一步中得到进一步的改进。
- 有监督的UIL学习
利用标记的锚定节点,通过玩双重学习游戏来改进映射函数Φ和\(Φ^{-1}\)。具体的,假设h个batches和n个anchor nodes,其中每个batch有\(\lfloor n/h \rfloor\)个标记的节点。每个batch组成了一个episode,其中一个anchor node \(u_a\)表示一个状态\(s_a\)。请注意,在这种情况下的状态转换是确定性的,当前状态的概率为1转移到下一个状态(锚节点),该操作被定义为选择一个锚节点。我们使用\(v(u_a)\)和\(v'(u_a)\)分别表示\(u_a\)在网络\(G^s\)和网络\(G^t\)中的向量表示。给定一个batch的anchor nodes,两个mapping func需要尽力根据批处理中映射锚定节点的奖励,对齐两个用户潜在空间。
对于一个从在\(G^s\)中的\(u_a\)开始的游戏。我们使用\(\Phi\)来映射它的向量到\(G^t\)的空间中,并且搜索其k个最邻近的向量\(S(v'(u_a))=Top(\Phi(v(u_a)))\),包含Gt中锚定节点最相似的k个嵌入向量。这里,k个向量是真实用户的候选,在更多锚节点上训练,成功链接的概率更高。在\(G^t\)中的agent B随后可以计算一个奖励\(r^i_{s,t}\):
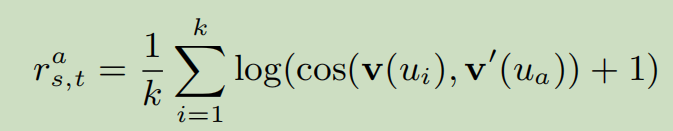
寻找并且平均topk的\(\Phi(v(u_a))\)的原因在于映射函数很难精确地匹配\(u_a∈G^t\)(向量\(v'(u_a)\))的实恒等式,然而,它有一个更大的概率在前k最近的k中包含真实的恒等式。
直观的,我们也可以计算\(v'(u_i)\)的映射返回\(G^s\),并且利用映射的二重性来产生第二个奖励\(r^a_{(t,s)}\)也就是\(\Phi^{-1}(v'(u_i))\)与\(v(u_a)\)之间的平均相似度。
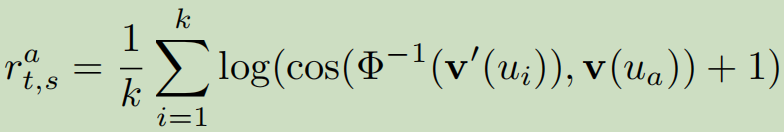
因此,动作值\(r^a\)对于一个选定的用户\(u_a\)来说就是\(r^a_{s,t}, r^a_{t,s}\)的线性组合,表明映射函数正确实身份链接的估计概率。特别是,它利用两个映射函数的对偶性来指导锚定节点的训练过程。期望的奖励\(E[r_h]\)在第h轮的batch是:
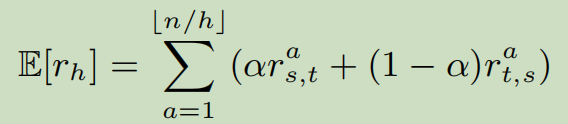
由于这个游戏的奖励可以被认为是\(v'(u_a),v(u_a),\Phi,\Phi^{-1}\)的函数,我们可以在最大化期望奖励的两个映射函数中优化参数W和b,其中\(\gamma^h_{s,t}\)以及\(\gamma^h_{t,s}\)是使用政策梯度法的贴现率。
我们也使用同样的方法从另一个方向训练深度Gs→Gt,以缓解过拟合。根据经验,我们发现平均连锁结果是有帮助对齐的 有效地连接两个网络。
最终本文的deeplink算法为:

