1. 摘要
现有的大多数的处理网络用户对齐的方法主要集中在如何最好地利用网络拓扑和属性信息以及利用已知的anchor links。尽管如此,除了少数例外,如何通过积极获得高质量和信息丰富的锚点链接来提高对齐性能还没有得到很好的研究。关于主动网络对齐的稀疏文献引入了循环中的人来标记一些种子节点的对应关系(即锚定链接),从查询潜在匹配的最不确定的节点的角度来看,这些是有用的。然而,内在网络属性信息对对齐结果的直接影响在很大程度上仍然是未知的。在本文中,作者提出了一种主动网络对齐方法(Attent)来确定最佳的查询节点。该方法的关键思想是利用定义在对齐解决方案上的有效的影响函数来评估供查询的候选节点的优度。
论文介绍
网络对齐的对齐准确度是最重要的,因为其对下游的应用有至关重要的作用,如对齐网络中相同的用户。
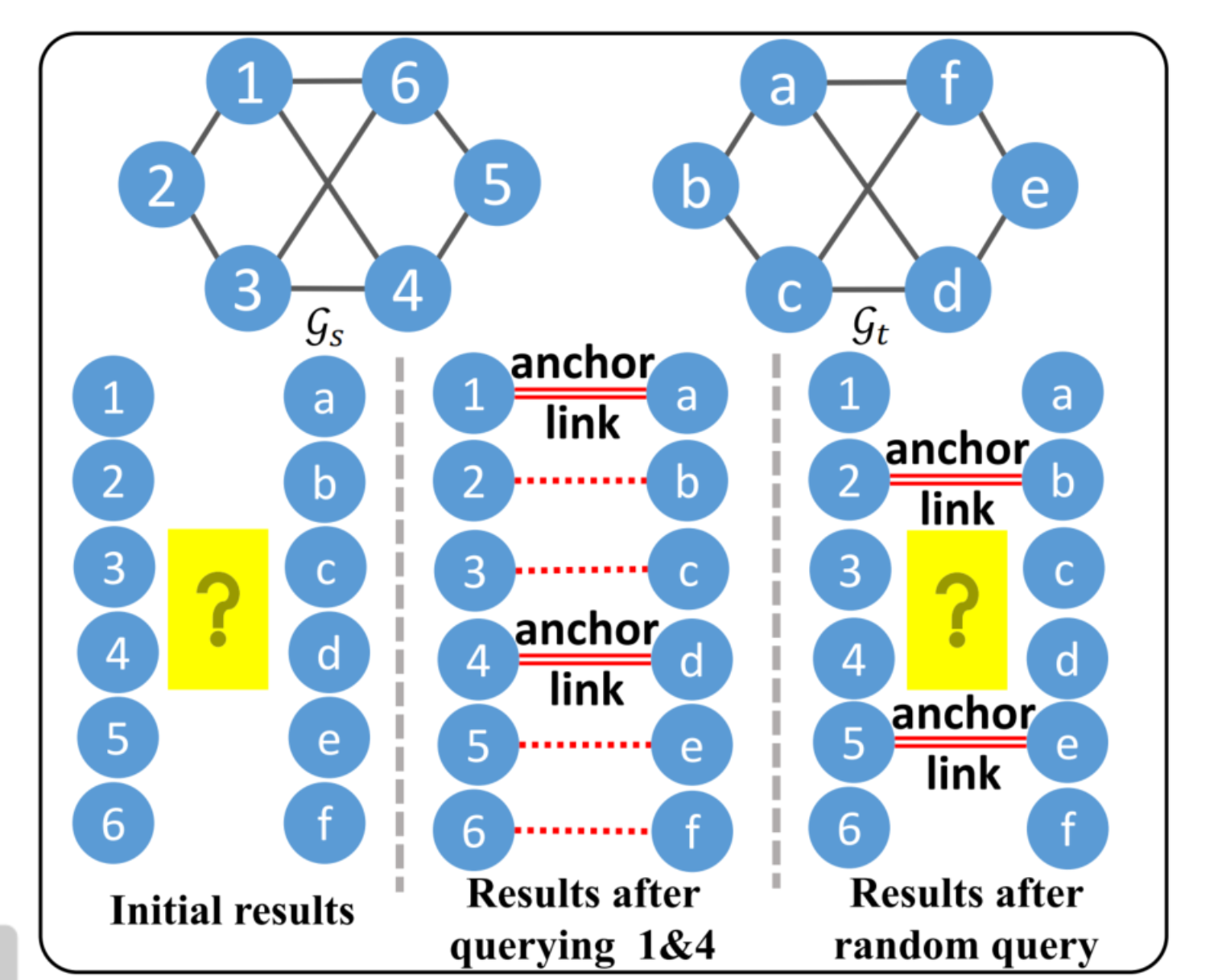
上面的图像就说明了,选取的anchor links是很重要的。如果选择的是节点1和4及其对应的已知锚定节点a和d,那么其余的节点就能根据拓扑的一致性来连接。但是如果选择的是2和5及其对应的节点b和e,那么剩下的节点1,3,4,6就不能被对齐,因为节点1还是可能连接a或者c。(分析一下拓扑结构就可以发现了)
网络对齐是一种受约束的二次分配的问题,是NP hardness的,网络对齐的应用性通常被对齐精度所约束。对于如何主动获得高质量的锚链路,以进一步提高广泛的网络对齐精度,网络对齐算法尚未得到很好的研究。关于主动网络对齐的稀疏文献通过引入人工注释器来标记给定查询的正确匹配来解决一些锚链接可用时的这个问题。 查询节点的选择是由边际概率分布(即找到真实对齐的确定性)决定的。这种方法是查询具有高不确定性的节点。
现有的查询策略主要存在三个问题:
- 查询对对齐结果的直接影响没有得到很好的研究,因为要查询的节点的选择依赖于对齐的抽样结果
- 网络属性信息如何改进主动网络对齐中的查询策略还没有深入研究
- 根据特定的采样策略,它可能具有较高的计算复杂度(如TopMatchings)
本文作者提出了一种基于影响函数的查询策略(Attent),根据查询对网络对齐结果的影响,主动归属网络对齐,向人工注释者建议最佳的查询,以标记正确的对齐。该查询方法的关键思想是利用定义在网络对齐结果上的影响函数来评估要查询的候选节点的优度。具体来说就是,给定了来自归属网络对齐算法的对齐解向量,我们将查询的信息量量化为我们提出的效用函数对有关查询的对齐结果的变化速率。
主动学习:在模型性能达到前提的情况下,尽可能减少标注样本。主动学习包含五个核心部分:未标注样本池、筛选策略、标注者、标注数据集、目标模型。主动学习将上述五个部分组合到一个流程中,直到目标模型达到预设的性能或者不再提供标注数据为止。主动学习也被应用在网络中。比方说基于不确定性,影响被应用于选择一个batch的探寻节点来标注,以此最大化网络分类的性能。
本文的一些符号定义如下:
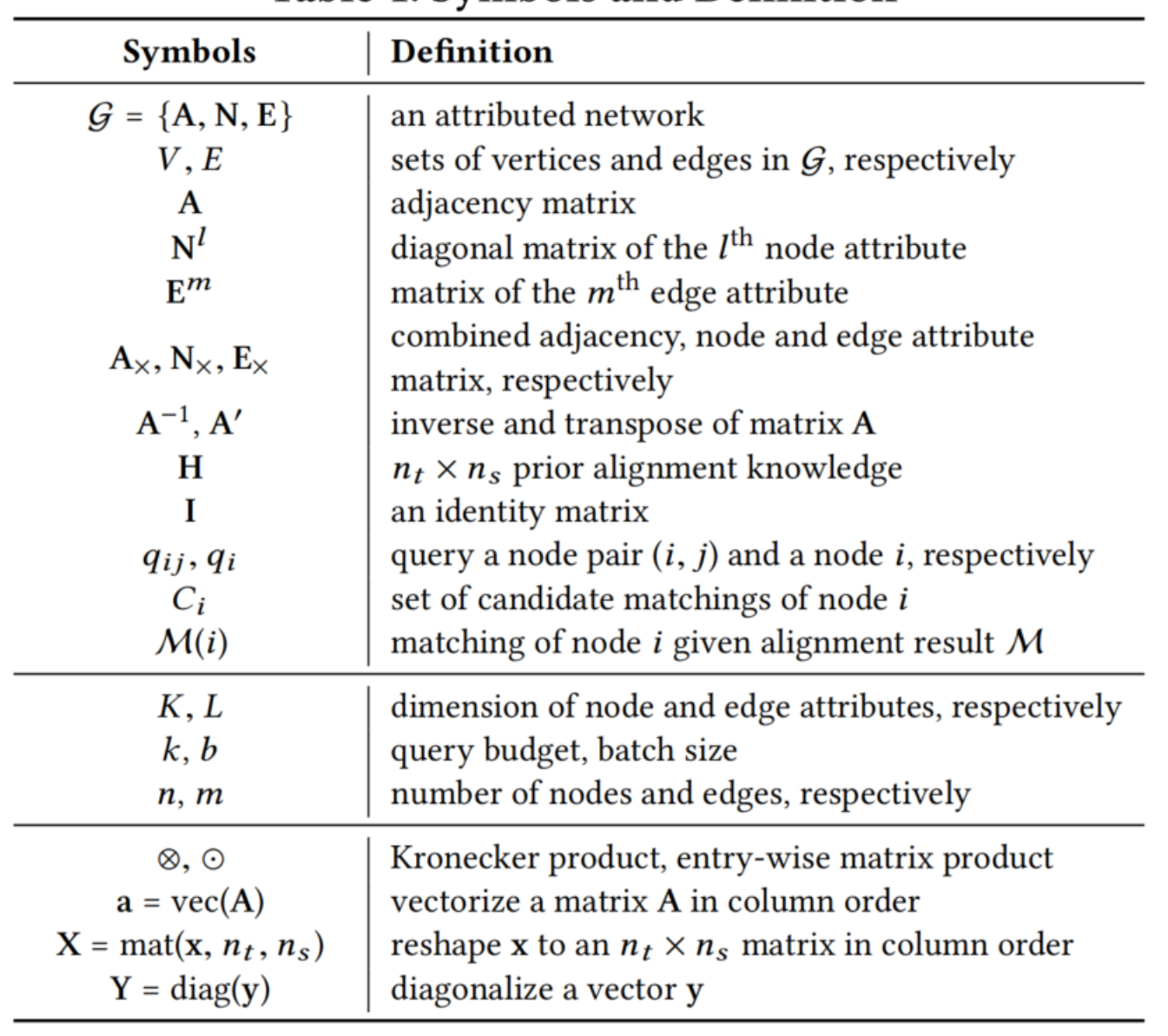
Kronecker product:
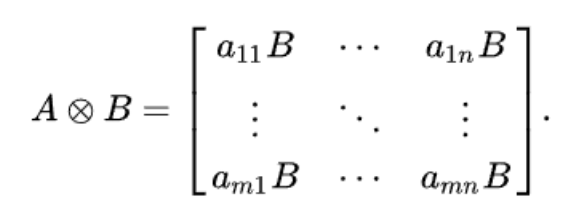

属性网络对齐:对齐两个网络的关键在于在三个方面的一致性(1)拓扑,(2)节点属性,(3)边属性。从优化的角度来看,归属网络对齐的目的是找到一个表示跨网络节点相似度的解矩阵X∈\(R^{n_t\times b}\),以最小化在上述三个方面中的不一致性 ,通过求解以下方程,得到了解矩阵的向量化,即x=vec(X)
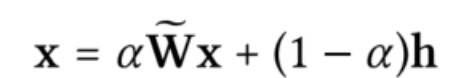
\(h=mat(H,n_t,n_s)\),\(H∈R^{n_s\times n_s}\)是对齐偏好矩阵,表示跨两个输入网络的首选节点相似性,\(α∈(0,1)\)是一个正则化参数,它决定了对齐结果向量x与偏好向量h的距离,\(\tilde{W}\)编码拓扑结构,节点属性和边属性一致性的矩阵,\(\tilde{W}=D^{-1/2}WD^{-1/2}\)表示\(W=N_X(E_X\cdot A_X)N_X\)。用于归一化W的对角线矩阵D被定义为:
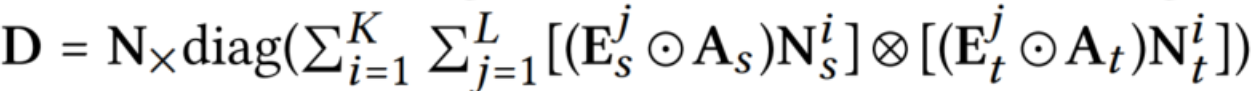
由于Kronecker product的特性,\(vec(ABC)=(C'\otimes A)vec(B)\),解向量可以被表示为:
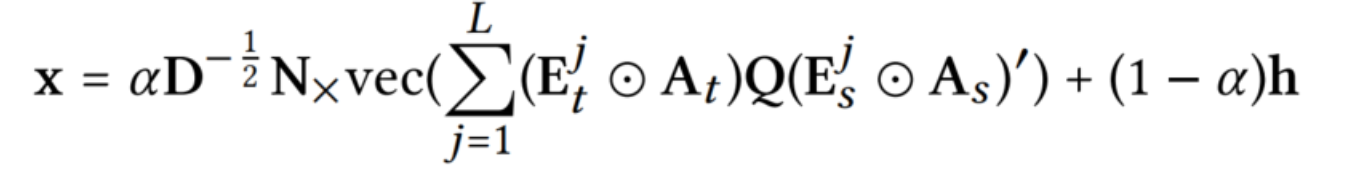
Q是经过重构\(q=N_XD^{-1/2}x\)在列顺序中定义的一个矩阵。如果节点和变得属性信息缺失了,那么x退化为:
\(x=αD_n^{-1/2}A_XD_n^{-1/2}x+(1-α)h\),其中\(D_n=diag([A_s1]\otimes A_t1)\),1表示的是全1向量。
对齐偏好矩阵H包含两个输入网络的两个节点相似的先验知识。比方说,对于节点p,q在\(G_s\)和\(G_t\)中
