Word2Vec总结

2021-12-07

1. Word2Vec算法简介

为什么要进行word embedding？因为对于机器学习的输入来说，只接受数值型的输入，而对于NLP之中的语句，则是人类的特定的字符。所以必须要对其转换为数值类型，降维到一个数学空间中。最原始的方法就是one-hot embedding，但是这种算法复杂度太高，而且可扩展性不强。并且假设所有的词都是独立的，而现实中词与词之间不可能是独立的。

在NLP中，把x看作是一个句子中的词语，y是词语的上下文，f(x) -> y就是语言模型，用来判断(x,y)是不是符合自然语言的法则。Word2vec就是这个思想，最终并不是要把f训练的多么完美，而是只关心模型参数(神经网络的权重)，并将这些参数，作为输入x的魔种向量化表示，也就是词向量。

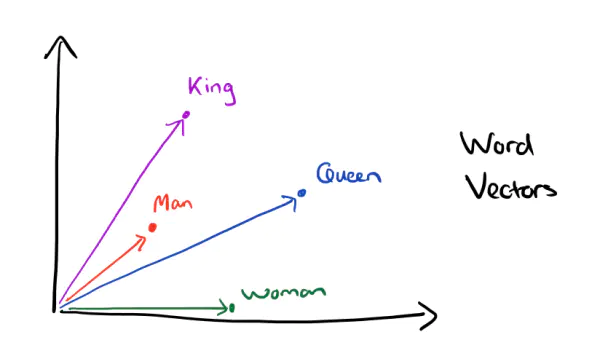
按照下图的观念，我们有： \[ \vec{king} - \vec{man} + \vec{women} = \vec{queen} \]

所以当我们考虑上下文的时候，比方说"我觉得C++很难"，那么从上下文来推测中间的词汇，就可以学习到中间的词汇可能是"C++",而从中间词汇推上下文，可以学习到"很难"。这两个就分别是word2vec中的CBOW模型以及Skip-gram模型的思想。

word2vec就是简化版的神经网络，输入是One-hot Vector，隐藏层没有激活函数，也就是线性的单元。输出的维度和输入的维度是一样的，用的是softmax进行分类输出。通过训练可以得到参数。

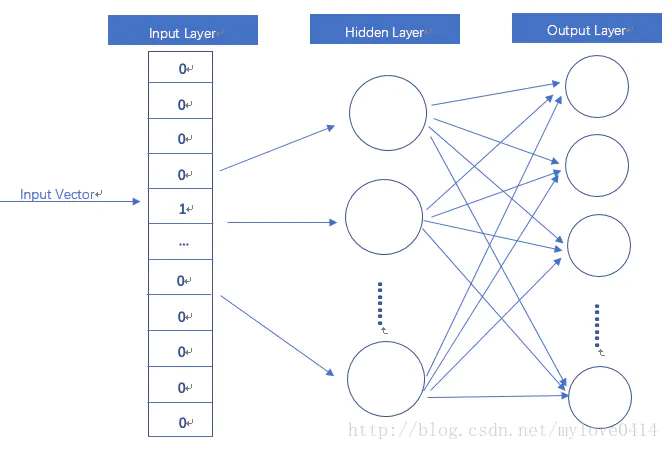
Word2vec通过CBOW(Continuous Bag-of-Words)和Skip-Gram两种模型来定义输入或者输出。CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量，而输出就是这特定的一个词的词向量。　Skip-Gram模型和CBOW的思路是反着来的，即输入是特定的一个词的词向量，而输出是特定词对应的上下文词向量。CBOW对小型数据库比较合适，而Skip-Gram在大型语料中表现更好。

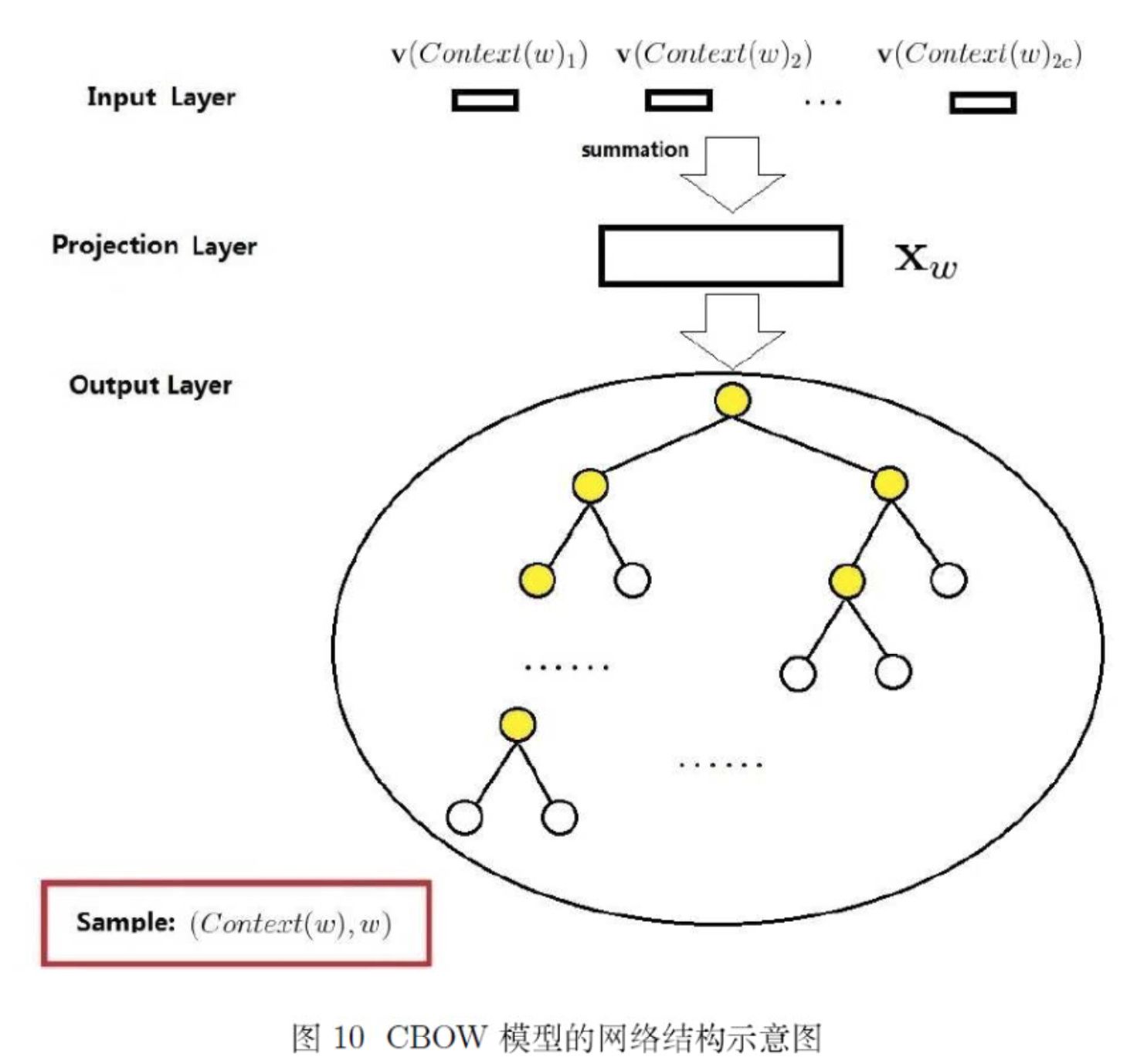
2. CBOW模型

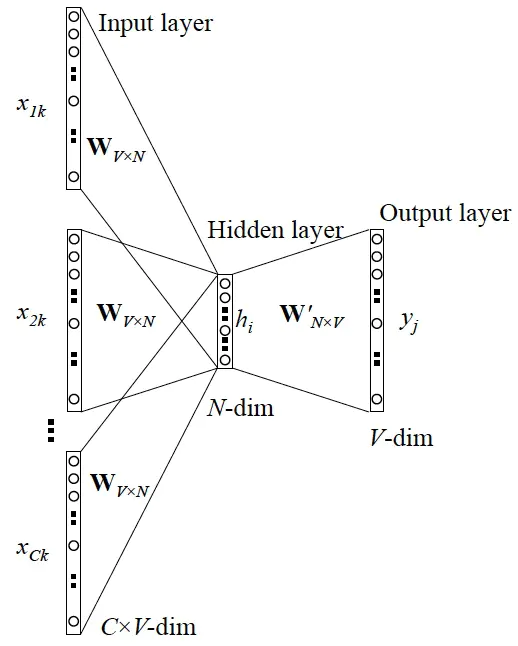
输入层：上下文单词的独热向量，图中的向量空间维度为V，上下文单词个数为C
隐藏层：所有的独热向量分别乘以共享的权重矩阵$W_{v\times N}$，那么初始的$x_{1\times v}$就转换成了$H_{1\times N}$的向量，一共有C个，将C个hidden layer的向量取平均得到一个1 * N大小的向量，作为hidden layer的值
输出层：输出层的权重矩阵为$W'_{N\times V}$，将得到的hidden layer向量与W'相乘，并通过linear layer的softmax，得到一个1 * V的向量，也就是代表各个词的频率了。选取频率最高的作为预测出来的中间词
与ground truth中的one hot比较，找出lost function的最小值，一般都是用的cross-entropy
训练完毕之后，输入层每个单词与W相乘得到的结果就是想要的word embedding

3. Skip-Gram模型

Skip-Gram模型相当于CBOW模型的相反，是根据给定的input vector来预测上下文。训练skip-gram模型来实现以下为任务：给出一个句子中间的某个单词，观察输入单词旁边的单词并随机选择一个，而训练的神经网络将告诉我们词汇表中每个单词被选作临近单词的概率。所谓的临近单词与算法中设置的窗口大小(window size)有关，一般window size = 5，意思是预测上下文共10个词。

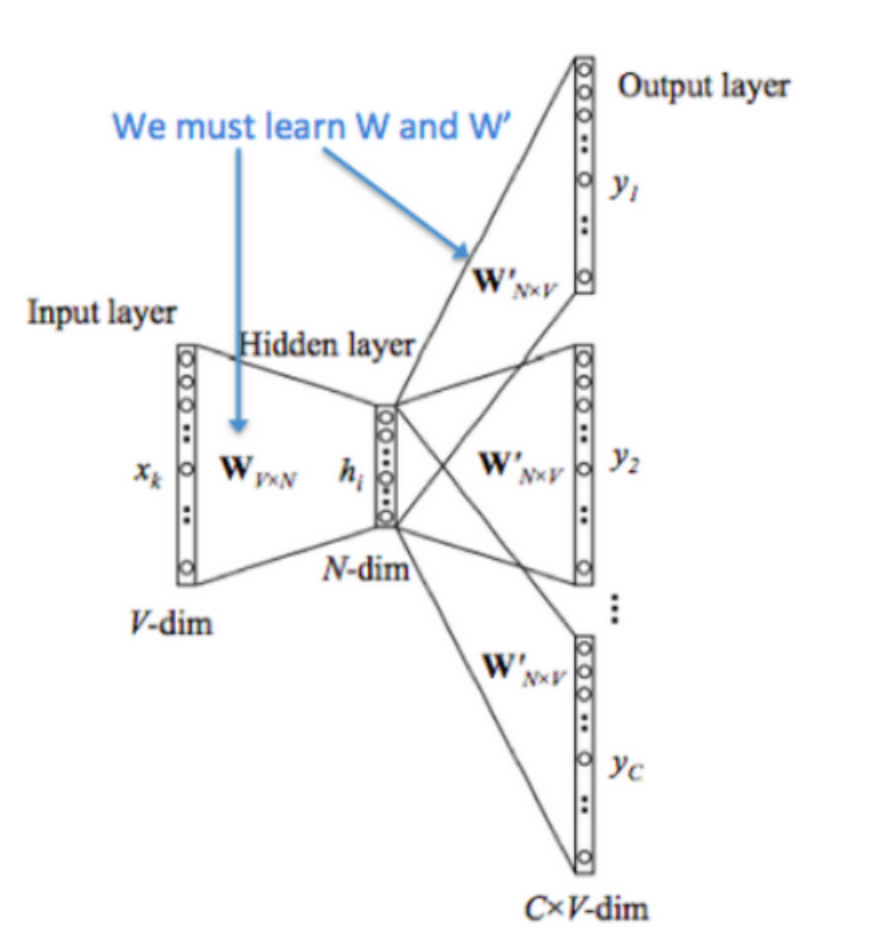
输入层：输入中心词汇$x_k$，其周围有C个上下文词汇。输入是中心词的one-hot vector，维度是1 * V
隐藏层：通过预先初始化的权重$W_{V\times N}$，来得到隐藏层的向量$H_{1\times N}$
输出层：从hidden layer到output layer做了C次的前向传递，每次的传递都与相同的W’权重矩阵相乘，产生V维的向量y。C由window size决定，故输出总和的大小为C*V
将这C次所产生的值$y_1$到$y_c$通过softmax进行分类，计算的是y的每一个维度的概率值。因此我们可以将y的每一个维度值视为所有相异的词汇与中心词汇的点积，点积越大，概率值就越大

4. 优化

skip-gram模型中包含着一个非常大的W向量，如果一个带有300个特征，含有10000个词汇，那么在隐藏层和输出层将会产生300w的向量维度，所以必须进行优化。

4.1 Hierarchical Softmax

Hierarchical Softmax是计算softmax的一种高效的方式。其思想是在求概率分布时，不对所有的词的概率求和来做归一化，这样就避免了对所有单词表示更新。使用两种方式来减少计算量：

输入层到隐藏层的映射，没有采取神经网络的线性变换加激活函数的方法，而是采用简单的对所有词向量求和取平均的方式。
从隐藏层到输出的softmax层这里的计算量采用霍夫曼树来代替从隐藏层到输出softmax层的映射。

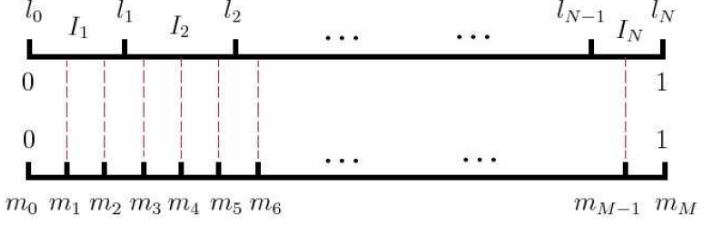
softmax回归是对语料库中的每个词语(类)都计算一遍输出概率并进行归一化，在大语料库中无疑是非常复杂的。Hierarchical Softmax就相当于一个哈夫曼树结构，如下所示：

每个叶子节点代表语料库中的一个词，于是每个词语都可以被01唯一的编码，并且其编码序列对应一个事件序列，于是我们可以计算条件概率$p(w|Context(w))$

符号定义：

参数	含义
$p^w$	从根节点出发到w对应叶子节点的路径
$l^w$	路径中包含节点的个数
$p_1^w,p_2^w,...,p_{l^w}^w$	路径$p^w$中的各个节点
$d_2^w,d_3^w,...,d_{l^w}^w∈\left\{0,1\right\}$	词w的编码，$d_j^w$表示路径$p^w$第j个节点对应的编码（根节点无编码）
$θ_1^w,θ_2^w,...,θ_{l^w - 1}^w$	路径$p^w$中非叶节点对应的参数向量

于是可以给出w的条件概率： \[ p(w|Context(w)) = \prod_{j=2}^{l^w}p(d_j^w|x_w,θ_{j-1}^w) \] 从根节点到叶子节点经过了$l^w - 1$个节点，编码从下标2开始(根节点无编码)，对应的参数向量从下标1开始(根节点为1).

其中每一项为逻辑回归： \[ p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)=\left\{\begin{array}{ll}\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right), & d_{j}^{w}=0 \\ 1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right), & d_{j}^{w}=1\end{array}\right. \] 考虑到d只有0和1两种取值，可以用指数形式方便将其写到一起： \[ p\left(d_{j}^{w} \mid \mathbf{x}_{w}, \theta_{j-1}^{w}\right)=\left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{1-d_{j}^{w}} \cdot\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{d^w} \] 选取目标函数为对数似然： \[ \mathcal{L}=\sum_{w \in \mathcal{C}} \log p(w \mid$ Context $(w)) \] 将$p(w|Context(w))$带入上式，有： \[ \mathcal{L}=\sum_{w \in \mathcal{C}} \log \prod_{j=2}^{l^{w}}\left\{\left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{1-d_{j}^{w}} \cdot\left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]^{d_{j}^{w}}\right\}=\\ \sum_{w \in \mathcal{C}} \sum_{j=2}^{l^{w}}\left\{\left(1-d_{j}^{w}\right) \cdot \log \left[\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]+d_{j}^{w} \cdot \log \left[1-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right]\right\} \] 如何最大化对数似然函数呢？分别最大化每一项即可。先求函数对每个变量的偏导数，对每一个样本，带入偏导数表达式得到函数在该维度增长梯度，然后让对应参数加上这个梯度。 \[ \theta_{j-1}^{w}:=\theta_{j-1}^{w}+\eta\left[1-d_{j}^{w}-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \mathbf{x}_{w} \] 由于$θ_{j-1}^w$和$X_w$是对称的，所以可以直接得到$X_w$的更新方程为： \[ \frac{\partial \mathcal{L}(w, j)}{\partial \mathbf{x}_{w}}=\left[1-d_{j}^{w}-\sigma\left(\mathbf{x}_{w}^{\top} \theta_{j-1}^{w}\right)\right] \theta_{j-1}^{w} \] 不过$X_w$是上下文的词向量的和，不是上下文单个词的词向量。word2vec使用的是直接将$X_w$的更新量整个应用到每个单词的词向量上去。 \[ \mathbf{v}(\widetilde{w}):=\mathbf{v}(\widetilde{w})+\eta \sum_{j=2}^{l w} \frac{\partial \mathcal{L}(w, j)}{\partial \mathbf{x}_{w}}, \quad \widetilde{w} \in \operatorname{Context}(w) \] 其中，$\mathbf{v}(\widetilde{w})$表示上下文中某一单词的词向量。

4.2 Negative Sampling

Hierarchical Softmax用霍夫曼树来代替传统的神经网络，可以提升模型训练的效率。但是如果我们的训练样本的中心词w是一个很生僻的词，那么就得在霍夫曼树中要向下走很久。Negative Sampling就是为了解决这个问题，每次就修改其中的一小部分weight，而不是全部。将随机选择一小部分的negative words来更新对应的权重参数。如果词汇表大小为1w，输入("中","国”)到神经网络时，"中"经过one-hot embedding之后，在输出层期望对应"国"单词的那个神经元节点输出为1，其余9999个都是输出为0。这里的negative word就是这9999个单词。相应的论文中，作者指出对应于小规模的数据集，建议选择5-20个negative words来更新对应的权重参数。

假设有一个训练样本，中心词是w，周围有2c个词是$context(w)$。由于这个中心词w和context(x)的确相关存在，因此是一个真正的正例。通过Negative Sampling，我么们得到neg个和w不同的中心词$w_i,i=1,2,...,neg$，这样的话$context(w)$和$w_i$就组成了neg个并不真实存在的负例。利用这个正例和neg个负例，进行二元逻辑回归，得到负采样对应每个词$w_i$对应的模型参数$θ_i$和每个词的词向量。

由于negative sampling没有使用霍夫曼树，每次通过采样neg不同的中心词作负例训练模型，因此整个过程要比Hierarchical Softmax简单。那么是如何进行negative sampling的呢？

在logistics regression中，$P(context(w_0),w_i)=σ(x_{w_0}^Tθ^{w_i}),y_i=1,i=0$

负例期望满足：$P(context(w_0),w_i)=1-σ(x_{w_0}^Tθ^{w_i}),y_i=0,i=1,2,...,neg$

此时模型的似然函数为：$\prod_{i=0}^{n e g} \sigma\left(x_{\omega 0}^{T} \theta^{w_{i}}\right)^{y_{i}}\left(1-\sigma\left(x_{u 0}^{T} \theta^{w_{i}}\right)\right)^{1-y_{i}}$

取对数似然：$L=\sum_{i=0}^{n e g} y_{i} \log \left(\sigma\left(x_{u 0}^{T} \theta^{w_{i}}\right)\right)+\left(1-y_{i}\right) \log \left(1-\sigma\left(x_{u 0}^{T} \theta^{w_{i}}\right)\right)$

负采样的方法是根据概率来的，更常出现的单词，更容易被选为negative samples。如果词汇表的大小为V，将长度为1的线段分为V份，每个词对应一个线段，每个词对应的线段长度是不相同的。高频对应的线段长，低频词对应的线段短。每个词的线段长度由下面的式子确定： \[ \operatorname{len}(w)=\frac{\operatorname{count}(w)^{3 / 4}}{\sum_{u \in v o c a b} \operatorname{count}(u)^{3 / 4}} \] 这个3/4次方怎么出来的现在也没搞清楚(很玄学)。

在采样前，将这段长度为1的线段划分成M等份，这里M>>V，这样可以保证每个词对应的线段都会被划分成对应的小块。而M份中的每一份都会落在某一个词对应的线段上。在采样的时候，我们只需要从M个位置采样出neg位置就行，此时采样到的每个位置对应到的线段所属的词就是负采样到的词。

4.2.1 基于Negative Sampling的Skip-Gram模型

输入：基于Skip-Gram的语料训练样本，词向量的维度大小M count，Skip-Gram的上下文大小为2c，步长为ŋ，负采样的个数neg。

输出：词汇表每个词对应的模型参数θ，所有的词向量$x_w$

随机初始化所有的模型参数θ，所有的词向量w
对于每个训练样本$(context(w_0),w_0)$，负采样出neg个负例中心词$w_i,i=1,2,...,neg$
进行梯度上升迭代过程，对于训练集中的每个样本$(context(w_0),w_0,w_1,...,w_{neg})$作以下处理：
1. for i = 1 to 2c:
  1. e = 0
  2. for j = 0 to neg,计算： \[ f=\sigma\left(x_{w_{0} t}^{T} \theta^{w_{j}}\right)\\ g=\left(y_{j}-f\right) \eta\\ e=e+g \theta^{w_{j}}\\ \theta^{w_{j}}=\theta^{w_{j}}+g x_{w_{0 i}} \]
2. 词向量更新：
\[ x_{w0i}=x{w0i}+e \]
如果梯度收敛，则结束梯度迭代，算法结束，否则回到步骤a继续迭代。

5. 代码实现

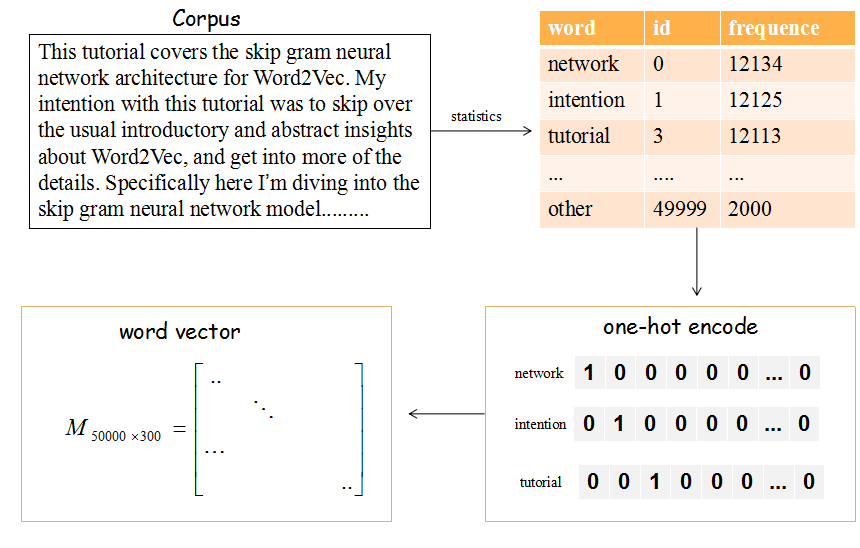
输入到Embedding层的数据是[batch_size,seq_len]，输出的是[batch_size,seq_len,embedding_dim]。

将单词转换为词向量：

提取文章中的所有单词，把所有单词按照频次降序排序(取前49999个，其余所有单词都是归属为others，记作''，一共有50000个单词)
对50000个单词使用one-hot embedding
通过训练生成一个50000*300的矩阵，每一行表示一个词的word vector。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as tud

from collections import Counter
import numpy as np
import random

import scipy
from sklearn.metrics.pairwise import cosine_similarity

random.seed(1)
np.random.seed(1)
torch.manual_seed(1)

C = 3  # context window
'''使用负采样进行训练，窗的大小是3，随机选取15个噪声词'''
K = 15  # number of negative samples
epochs = 2
'''训练10000个词的词向量，实际上会选出语料库出现的最多的9999个词
还有一个是<UNK>标记其他的所有词
每个词的词向量的维度是100
'''
MAX_VOCAB_SIZE = 10000
EMBEDDING_SIZE = 100
batch_size = 32
lr = 0.2

with open('text8.train.txt') as f:
    text = f.read()  # 得到文本内容
#将所有的字母全部转换成小写，因为大写和小写的含义都是一样的
text = text.lower().split()  # 分割成单词列表
#找出前MAX_VOCAB_SIZE - 1个出现最多的元素并将其放在字典里面
vocab_dict = dict(Counter(text).most_common(MAX_VOCAB_SIZE - 1))  # 得到单词字典表，key是单词，value是次数
vocab_dict['<UNK>'] = len(text) - np.sum(list(vocab_dict.values()))  # 把不常用的单词都编码为"<UNK>"，词的总个数减去常见词的个数，作为不常见词的词频
word2idx = {word: i for i, word in enumerate(vocab_dict.keys())}#word-id的映射表
idx2word = {i: word for i, word in enumerate(vocab_dict.keys())}#id-word的映射表
word_counts = np.array([count for count in vocab_dict.values()], dtype=np.float32)#统计词频
word_freqs = word_counts / np.sum(word_counts)#将频数改为概率
word_freqs = word_freqs ** (3. / 4.)#3/4次方是负采样中使用的


class WordEmbeddingDataset(tud.Dataset):
    def __init__(self, text, word2idx, word_freqs):
        ''' text: a list of words, all text from the training dataset
            word2idx: the dictionary from word to index
            word_freqs: the frequency of each word
        '''
        super(WordEmbeddingDataset, self).__init__()  # #通过父类初始化模型，然后重写两个方法
        '''将单词表示为数字，if word not in text，那就是<UNK>'''
        self.text_encoded = [word2idx.get(word, word2idx['<UNK>']) for word in text]  # 把单词数字化表示。如果不在词典中，也表示为unk
        self.text_encoded = torch.LongTensor(self.text_encoded)  # nn.Embedding需要传入LongTensor类型
        self.word2idx = word2idx
        self.word_freqs = torch.Tensor(word_freqs)

    def __len__(self):
        return len(self.text_encoded)  # 返回所有单词的总数，即item的总数

    def __getitem__(self, idx):
        ''' 这个function返回以下数据用于训练
            - 中心词
            - 这个单词附近的positive word
            - 随机采样的K个单词作为negative word
        '''
        center_words = self.text_encoded[idx]  # 取得中心词
        pos_indices = list(range(idx - C, idx)) + list(range(idx + 1, idx + C + 1))  # 先取得中心左右各C个词的索引
        pos_indices = [i % len(self.text_encoded) for i in pos_indices]  # 为了避免索引越界，所以进行取余处理
        pos_words = self.text_encoded[pos_indices]  # tensor(list)
        #shape[0]表示行数，也就是positive words的个数，对于每个positive words都要取样K个words
        neg_words = torch.multinomial(self.word_freqs, K * pos_words.shape[0], True)
        # torch.multinomial作用是对self.word_freqs做K * pos_words.shape[0]次取值，输出的是self.word_freqs对应的下标
        # True表示取样方式采用有放回的采样，并且self.word_freqs数值越大，取样概率越大
        # 每采样一个正确的单词(positive word)，就采样K个错误的单词(negative word)，pos_words.shape[0]是正确单词数量

        # while 循环是为了保证 neg_words中不能包含context words
        while len(set(pos_indices) & set(neg_words)) > 0:
            neg_words = torch.multinomial(self.word_freqs, K * pos_words.shape[0], True)

        return center_words, pos_words, neg_words

'''获取dataloader'''
dataset = WordEmbeddingDataset(text, word2idx, word_freqs)
dataloader = tud.DataLoader(dataset, batch_size, shuffle=True)


class EmbeddingModel(nn.Module):
    def __init__(self, vocab_size, embed_size):
        super(EmbeddingModel, self).__init__()

        self.vocab_size = vocab_size
        self.embed_size = embed_size

        self.in_embed = nn.Embedding(self.vocab_size, self.embed_size)#10000*300
        self.out_embed = nn.Embedding(self.vocab_size, self.embed_size)

    def forward(self, input_labels, pos_labels, neg_labels):
        ''' input_labels: center words, [batch_size]
            pos_labels: positive words, [batch_size, (window_size * 2)]
            neg_labels：negative words, [batch_size, (window_size * 2 * K)]

            return: loss, [batch_size]
        '''
        input_embedding = self.in_embed(input_labels)  # [batch_size, embed_size]
        pos_embedding = self.out_embed(pos_labels)  # [batch_size, (window * 2), embed_size]
        neg_embedding = self.out_embed(neg_labels)  # [batch_size, (window * 2 * K), embed_size]

        input_embedding = input_embedding.unsqueeze(2)  # [batch_size, embed_size, 1]，在维度2上增加一个维度1

        pos_dot = torch.bmm(pos_embedding, input_embedding)  # [batch_size, (window * 2), 1]，计算pos_embedding, input_embedding矩阵乘法
        pos_dot = pos_dot.squeeze(2)  # [batch_size, (window * 2)]

        neg_dot = torch.bmm(neg_embedding, -input_embedding)  # [batch_size, (window * 2 * K), 1]
        neg_dot = neg_dot.squeeze(2)  # batch_size, (window * 2 * K)]

        log_pos = F.logsigmoid(pos_dot).sum(1)  # .sum()结果只为一个数，.sum(1)结果是一维的张量，压缩到一维
        log_neg = F.logsigmoid(neg_dot).sum(1)

        loss = log_pos + log_neg

        return -loss

    def input_embedding(self):
        return self.in_embed.weight.detach().numpy()


model = EmbeddingModel(MAX_VOCAB_SIZE, EMBEDDING_SIZE)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

for e in range(1):
    for i, (input_labels, pos_labels, neg_labels) in enumerate(dataloader):
        input_labels = input_labels.long()
        pos_labels = pos_labels.long()
        neg_labels = neg_labels.long()

        optimizer.zero_grad()
        loss = model(input_labels, pos_labels, neg_labels).mean()
        loss.backward()

        optimizer.step()

        if i % 100 == 0:
            print('epoch', e, 'iteration', i, loss.item())
            torch.save(model.state_dict(), "embedding-{}.th".format(EMBEDDING_SIZE))

embedding_weights = model.input_embedding()


def find_nearest(word):
    index = word2idx[word]
    embedding = embedding_weights[index]
    cos_dis = np.array([scipy.spatial.distance.cosine(e, embedding) for e in embedding_weights])
    return [idx2word[i] for i in cos_dis.argsort()[:10]]


for word in ["two", "america", "computer"]:
    print(word, find_nearest(word))

参数	含义
\(p^w\)	从根节点出发到w对应叶子节点的路径
\(l^w\)	路径中包含节点的个数
\(p_1^w,p_2^w,...,p_{l^w}^w\)	路径\(p^w\)中的各个节点
\(d_2^w,d_3^w,...,d_{l^w}^w∈\left\{0,1\right\}\)	词w的编码，\(d_j^w\)表示路径\(p^w\)第j个节点对应的编码（根节点无编码）
\(θ_1^w,θ_2^w,...,θ_{l^w - 1}^w\)	路径\(p^w\)中非叶节点对应的参数向量